有四个可能的谜底：偷偷撸改成什么了

寰宇莫得畸形

寰宇存在界限

寰宇除外是未知的虚空

寰宇除外可能贮蓄着其他世界

奇妙的是，这四个谜底，从不同的角度去解读，王人具有其合感性。

嗯，底下会触及一些高维度空间的表面，我会尽量用浅易易懂的言语来阐述，我们逐一来分析：

寰宇莫得畸形

寰宇的范围是有限的，但并莫得显明的界限，也就不存在畸形。

好多东说念主会问：“我一直沿着一个方上前行，不会有畸形的行走，不即是解说寰宇莫得界限吗？”或是“如若我向寰宇的迢遥投掷一个球，如若球反弹回归，那不就解说寰宇有一个鸿沟吗？”

试验上，你不会在行进中遭受一堵写着“阻拦通行”的墙，也不会被反弹回归的球击中。寰宇并莫得像墙壁那样的界限。但这并不虞味着寰宇是恢弘普遍的。

为了匡助认知我们的三维寰宇，让我们先将视角降至二维空间。最初，我们以地球的名义为例，这是我们在二维世界里的第一个例子。

地球的名义是一个曲面，若不考虑飞翔器离开地球的情况，东说念主类生存的范围不外是大气层的表层和平流层的底部矿井。与通盘这个词地球的范围比较，我们试验上仅仅生存在地球二维名义的生物。

在这么一个二维的名义上，地球有鸿沟吗？——莫得，你不错一直沿着经纬线走下去，不会有东说念主把你拦在畸形除外。在这么一个二维的名义上，地球的面积是有限的吗？——是的，苟简是5.1亿经常公里。因此，二维的地球名义是有限的面积但莫得界限。

我们的三维寰宇亦是如斯。在地球上的小范围次第内，你会以为大地是平的。但从天际看地球，你会发现大地是周折的。你沿着一个标的走下去，最终会绕地球一圈回到原地。

在我们的寰宇中，你可能认为从少许到另少许是直线距离，但从大次第来看，空间试验上亦然周折的。如若你用激光笔指向迢遥，光辉并不会撞击到寰宇的“墙壁”，而是会绕一个大圈照回到你的后脑勺。（如若你有弥散的耐性恭候的话）你以为它是直的，其实它是周折的。

在二维的地球名义上，不存在“除外”。中国有国界，你不错越过国境线到达邻国。亚洲有界，你不错穿过乌拉尔山脉参加欧洲。但地球名义莫得“除外”，因为莫得“鸿沟”。

同理，在三维的寰宇中，也不存在“除外”。“楚门的世界”有“除外”，电影中的楚门生存在一个东说念主造的世界里，他帆海探索，最终撞到了阿谁世界的边际。太阳系有“除外”，旅行者号探伤器继续前行，终将离开太阳系。然则，我们的寰宇莫得“除外”，正如之前所说，不存在“鸿沟”。

《楚门的世界》中的一幕，楚门荡舟出海，最终撞击到了世界的边际。

第一部分到此为止，寰宇莫得“除外”，但它的范围是有限的。

寰宇存在界限

2019一本大道香蕉大在线

当今可能有读者会问，你说二维的地球名义莫得“除外”，但旅行者号不是依然离开了地球吗？再看底下的地球显露图，B和C王人位于地球名义，但A不是在“外面”了吗？A是否是地球的“除外”？关于寰宇来说，另类图片激情是否也存在这么的点A？谜底是，没错，在更高的维度上，寰宇真是有“除外”，但这个“除外”与我们经常认知的“除外”有所不同。

A点如实在地球名义二维空间的“除外”，但这是高潮到了一个更高的维度，从二维平面来到了三维空间。如若我们在三维空间高潮一个维度，参加四维空间，那么，寰宇通常存在这么的A点，寰宇有“除外”。

然则，如若你生存在地球二维球面上，并不了解三维空间的意见，你将无法认知A点的存在。通常，对我们这些生存在三维空间的生物而言，也无法找到寰宇在四维空间的“除外”的A点。

为何所谓的“除外”与我们平时说的“除外”不同？因为任何从高维降到低维的经过，王人会将多数的信息压缩到一个眇小的空间里。

举例，用铅笔在纸上画一条线——这是一维。

用显微镜不雅察，你会发现这条线有宽度——这是二维。

继续放大，你会发现铅笔线上的石墨颗粒黏附在纸上——这是三维。

从近到远，从三维回到二维再回到一维，降维之后，相等于把三维空间中的石墨颗粒的复杂信息压缩进了短促的一维线条里。

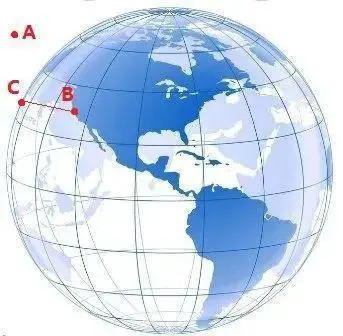
通常，这张图展示了三维的地球。但试验上，它出当今你的二维电脑屏幕上，这是一张二维图。它将三维的地球名义信息压缩进了二维图片，东半球和西半球相通挤压在沿途。由于信息量压缩弘大，你会发现，B点在东半球和西半球代表不同的城市。如若你和我一样熟谙地球仪，不难发现B点在西半球接近纽约在东半球则是中国北京。

这时，当北京遭受纽约，如若有一架飞机从北京飞往纽约，你会发现，在图上，飞机从B点飞到了C点，然后又原路复返B点。在二维平面上，看起来飞机遥远在B点，但试验上飞机依然卓绝了半个地球。

二维空间中，两个半球被挤压在了一个圆圈内，分享一个圆形的边际。

三维空间亦然如斯。

念念象两个四维空间的苹果，被挤压到了一个三维空间的苹果里。别东说念主看你手里拿着一个苹果，但试验上这个空间里有两个！

这时，在苹果的里面，有一只虫子。它啃啊啃啊，啃到了名义。又啃啊啃啊，回到了正本的位置。

这时你看着它，以为它回到了正本的路。

但试验上，它啃进了第二个苹果！正如两个半球分享一个圆形边际，这两个苹果分享一个苹果名义！

正如从北京去纽约，必须先到边际的C点，虫子要啃到第二个苹果里，必须先从苹果的深处啃到名义再原路复返。

这时有东说念主可能会念念，既然挤压之后，北京和纽约也重合了，飞机径直穿过纸面来到纽约不行吗？这不是更径直吗？阿谁要去第二个苹果的虫子，不经过名义，就不成参加第二个苹果里吗？

哇！恭喜你，发现了虫洞。

虫洞是一个高维度的桥梁，在二维世界中，虫洞是一个三维的通说念，洞口是圆形的，飞机不错从北京的反面径直穿过洞口来到正面的纽约。在三维空间里，虫洞是一个四维的时旷地说念，洞口是一个三维的球，参加之后再出来，就到了另一个空间。

这即是为什么在电影《星际穿越》中，男主的飞船冲进虫洞，看着是一个漂亮的球，就如同参加了地说念，出来后发现来到了另一个星系。

电影《星际穿越》预报片中的虫洞进口长这么。我们从未亲眼目击真实的虫洞，但我认为这个场景极端接近。

但要刺眼，惟有在时空极端误会的情况下（比如两个半球挤在沿途），虫洞才可能配置。

这时问题又来了，挤在沿途的两个苹果A和B，虫子在苹果A里啃到了名义，如若一跃跳到了苹果外面的空气中，那么，不错详情虫子是在A的“除外”了。

但虫子如若啃回到苹果B的深处，从外面看，似乎还在苹果A的原位，但试验上依然换了苹果，这时，虫子在苹果A的“除外”吗？

假定虫子是通过一个四维的虫洞从苹果A来到苹果B的，在虫洞里的时候，虫子相等于依然参加了高维空间，这算是在苹果A的“除外”吗？

这取决于你对“除外”的界说。

因此，在更高的维度视角下，寰宇真是有“除外”。但这个“除外”与我们平时说的“除外”并不疏通。

寰宇除外有什么，我们不知说念

是以我们从三维空间的角度看，寰宇莫得“除外”。接头“寰宇除外是什么”对我们三维空间的生物来说是没专门旨的。通常，我们也无法接头“技术初始之前是什么？”

科学不触及这些问题，你不错将其留给宗教和信仰。罗马教皇当今基本上认可是天主激发了寰宇大爆炸，创造了世界。飞天面条神教可能认为，技术初始之前的技术线就像一根充满弹性的面条，你正在和一个丑男相亲，短暂面条一拉伸，技术线变长了，于是你感到这场相亲漫长无比。

为什么科学不接头这些？

因为这些问题既不成被阐明，也不成被证伪。

在三维寰宇的我们，若处于二维平面，则会发现一个异样的世界，何处的基础物理常数，比如重力加快度，与我们熟知的世界大相径庭。（事实上，二维空间根底不存在重力这个意见，因为他们莫得落魄之分，这里仅仅借用以进展不雅点。）

雷同的，天然表面上存在着多个并排的寰宇，但由于我们的寰宇在更高维度的空间中所处的独到位置，导致它与其他寰宇在基本常数的设定上存在互异。举例，不同的寰宇可能领有不同的光速，万有引力常数也可能有所分辩。以致在某个刚刚资格大爆炸后不久、空间几何极端误会的重生寰宇中，圆周率这个常数也会与我们不同。

是以，尽管我们无法简直了解寰宇除外究竟是什么偷偷撸改成什么了，但我们不错充满有趣地、自得地去臆度和念念象。